| On this page |
Overview ¶
In Houdini, primitives refer to a unit of geometry, lower-level than an object but above points. Houdini supports several different types of primitives:
-
Packed primitives, Packed Disk primitives, and Packed Disk Sequence primitives
-
Polygon/Bezier/NURBS curves
There is also a special primitive called a packed primitive that represents a lightweight reference to geometry stored somewhere else. This is very useful for copying/instancing and working with heavy geometry. Alembic files are represented in Houdini as packed primitives.
There are also several quadratic primitive types that represent geometric figures mathematically rather than as polygonal surfaces. These may be useful as lightweight geometry:
-
Circle (defined by a single point, rotation, and radius)
-
Sphere/ellipsoid (defined by a single point and radii)
-
Tube/cone (defined by a single point, rotation, radii, and length)
Houdini’s Circle,
Sphere, and
Tube have parameters that allow you to choose whether to create, for example, a “primitive sphere” or a polygonal sphere.
You can convert most geometry types to other geometry types using the Convert SOP.
Tip
Press on a node in a geometry network to see a pop-up showing information about the geometry flowing through the node, including the number/types of primitives.
Polygons and meshes ¶
Polygons are shapes constructed from a series of straight edges. These edges are defined by a series of vertices. Polygons are ideal for dealing with complex topologies that go beyond the four sided nature of meshes and NURBS surfaces.
A mesh is a collection of polygons with guaranteed ordering. A mesh is much more efficient than the equivalent polygons, and unlike most regular polygons, you can convert a mesh directly to NURBS. You can also use the Convert SOP to convert mesh primitives to regular polygons when you want a nice layout of polygons in rows and columns.
Polygons have the following properties:
Open/Closed
A closed polygon shares its first and last vertex, and is flagged internally as “closed”. Only closed polygons are shaded.
Planar/Non-planar
Planar polygons' vertices lie in the same plane in 3D space. Non-planar polygons have vertices that do not all lie on a single plane in 3D space.
Convex/Concave
A polygon is convex if every infinite line (in the same plane as the polygon) intersects the polygon in at most two points. Concave polygons have more complex shapes with “inset” points.
Use the tools on the Create shelf tab to create surfaces. On the operation control toolbar above the viewport, choose an option from the Primitive Type menu to tell Houdini how to construct the polygon.

Use the tools on the Polygon shelf tab to edit and reshape faces and polygonal surfaces.
Packed primitives ¶
See packed primitives.
Polygon soup ¶
A polygon soup is a primitive that stores polygons using a compact memory representation, and very efficiently stores faces whose primitive attributes are the same. Its in-memory representation allows almost all the memory of a large soup to be shared between the nodes operating on the soup as long as the topology does not change. In contrast, regular polygons require each node to retain a copy of every polygon. This memory sharing also makes memory caches more efficient, resulting in generally faster modeling and rendering operations, in addition to less memory usage. The more polygons in a soup, the greater the benefit over regular polygons. For simple geometry with few polygons, the management overhead of soups can make them slower than regular polygons, although soups will always use less memory.
You can convert geometry to a polygon soup using the Polysoup node.
Loading a soup from a file can be much faster than loading regular polygons (for Mantra as well as Houdini). You can load Alembic files as polygon soups. Creating Grid,
Sphere,
Tube, and
Torus shapes is faster when you use the option to create soups.
Along with the shape nodes, you can create soups with Convert,
Convert Meta,
Convert VDB,
Convert Volume,
Iso Offset,
Point Cloud Iso,
Subdivide, and
Tetra Surface. You can use the
Subdivide node to subdivide soups if you choose one of the OpenSubdiv methods.
Many (but not all) geometry nodes can operate “natively” on polygon soups. You get the benefits of the soup’s sharing with operations that modify attributes, such as Edit,
Transform,
Sculpt,
Attribute Transfer onto points, point Group,
Attribute Create,
Attribute Wrangle,
Attribute Copy, computing point normals with
Facet, point
UV Project, Paint, Groups from Name, point
Connectivity, and
Ray, among others.
Some operations modifying vertex or primitive attributes may still work on polygon soups, but could have a slightly different meaning than for polygons. For example, each soup is only one primitive, so the polygons in a soup cannot have their own primitive attributes. Also, polygon soups often do not have as many vertices as polygon primitives (they merge identical vertices). This means that, for example, UV Project cannot compute vertex texture coordinates correctly, and cusping vertex normal isn’t supported.
Most operations that change polygon topology, such as Poly Extrude and
Poly Split, do not support soups, but a few do. For example, the Convex Polygons option on the
Divide node will convex a polygon soup and avoid adding any additional vertices, allowing the memory for the vertex attributes to be shared.
For nodes that do not support soups, you can use Convert to convert a soup to regular polygons, and then convert the polygons back to a soup using
Polysoup. However, the benefits of polygon soups is usually overwhelmed by the conversion cost, so in most cases, you should just use regular polygons. (If you are doing this type of conversion back and forth in an HDA, set the Unload flag on all nodes whose output is polygons, so the SOP cache won’t hold onto the polygons longer than necessary.)
See the section below for when to use polygon soups, packed primitives, or regular polygons.
Polygon soup vs. Packed primitives vs. regular polygons ¶
See also instancing using packed geometry and polygon soups.
Editing |
Regular polygons are supported by all operations in Houdini. Polygon soups are supported by many, but not all, operations in Houdini. The geometry of packed primitives is not editable or deformable. However, you can transform them and set attributes on the points that represent the packed geometry. |
Memory usage |
Packed primitives are only loaded into memory as needed. For packed primitives that reference a disk file, they are streamed directly to the graphics card for display and to the renderer for rendering. The ongoing memory usage of a packed primitive can often be zero. Polygon soups have a much more compact memory representation than regular polygons. Regular polygons use the most memory of the three. |
Tips |
For small pieces of geometry, use regular polygons to avoid the overhead of polygon soups. If you need to use any operations that change topology or don’t support polygon soups, use regular polygons all the way through, as the cost of converting from a soup to regular polygons usually overwhelms any benefit from using soups for only part of a node chain. If you have large geometry that you need to edit or deform, use polygon soups. If you only need to display and transform the geometry, store it on disk and use packed primitives. |
Interpreting memory usage ¶
You can see how much memory a node is using by pressing on the node. A pop-up will appear showing various ways of measuring the memory usage of the node:
Memory
The total amount of memory referenced by a particular detail. This memory may be shared with another node (for example, a polygon soup), so this is not necessarily how much memory you will save if you delete this node. It is more a measure of how much stuff is passing through the node.
New
The amount of memory referenced by this node that is not referenced by any of its inputs. This indicates how much memory is used by this node. This number is not reported for nodes without inputs (generators).
Unique
The memory that is only referenced by this node (that is, not referenced by its inputs or outputs). This indicates how much memory you would save if you turned on the Unload flag on this node.
This display has some limitations:
-
The memory referenced by packed primitives is not yet counted for performance reasons.
-
The SOP cache manager and the
Cache SOP do not yet track memory usage correctly.
-
Pressing
on a subnet (such as a digital asset) only shows the memory used by the subnet itself, not the memory usage of the network inside the subnet.
USD packed primitives ¶
Like Alembic packed primitives, USD packed primitives store foreign data (in this case, USD geometry) inside a SOP primitive. The viewport knows how to display the geometry encoded in these primitives, but if you want to modify the data inside, you first need to unpack it.
Points in the packed primitive represent USD prims, and the point position and standard point instancing attributes represent each prim’s transform. You can modify these to move/rotate/scale the prims without unpacking them. (This is common when working the RBD sims.)
Use the Unpack USD SOP to convert packed USD geometry into SOP geometry so you can modify it using subsequent SOP nodes. You can convert the USD geometry to polygons or packed SOP primitives. Unless you only want to use SOPs that work directly on packed primitives, you should choose to convert to polygons.
Metaballs ¶
Metaballs create an implicit surface computed around a set of points. Metaballs are like spheres centered around points. When two metaballs are placed near each other, their surfaces merge smoothly.
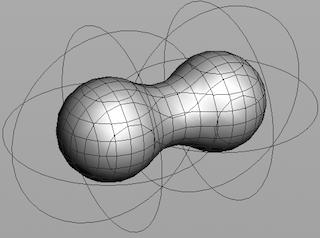
Metaballs may be useful for representing blobby or weird surfaces. You can also change how the surface is computed, which may be useful to achieve certain effects:


NURBS and Bezier splines ¶
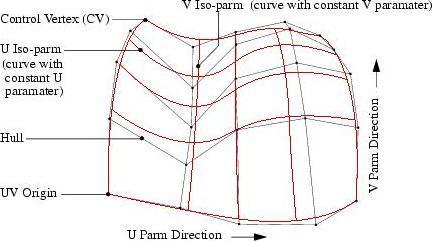
NURBS is an acronym for Non-Uniform Rational B-Spline. NURBS are smooth curves and surfaces defined by control vertices (CVs). See the Wikipedia definition for more information. The advantage of NURBS is that moving a CV reshapes the surrounding curve/surface while maintaining the continuity of the curve/surface. This allows you to “pull and tug” on the CVs of the NURBS curve or surface to generate a desired shape without causing kinks or discontinuities.
Bézier curves/surfaces are simpler than NURBS. See the Wikipedia definition for more information. Bézier curves allow discontinuities at the knots, making it easier to create corners, but harder to create smooth continuous curves/surfaces.
Parameterization ¶
The shape of a NURBS curve, given a set of CVs, is determined by the relative distance between knots. There are two types of knot parameterizations: uniform and chord length.
-
In uniform parameterization, knots are spaced evenly.
-
In chord length parameterization, the distances between knots are determined by the distances between successive CVs.
Uniform parameterization is recommended for regular shapes, while chord length is used for free-form shapes. A third type of parameterization called “centripetal” is similar to chord length, and is best suited for sharp curves.
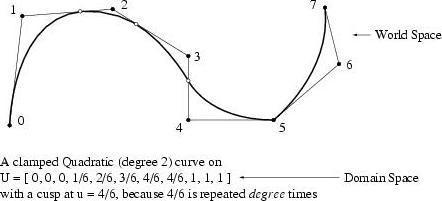
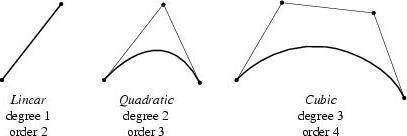
Order/degree ¶
Spline curves have an order , sometimes referred to as a degree, which is one less than the order. The degree determines the potential smoothness of the line. A polyline has degree 1 (or “second order”). A curve with one control point between knots has degree 2 (“third order” or “cubic”). The familiar Bézier curve, with two control points between knots, has degree 3 (“fourth order” or “quadratic”).
Houdini supports splines with degrees from 1 to 10. For animation and effects, degree 2 (cubic) splines are usually sufficiently smooth and well-behaved. You seldom need to use other degrees.
Creating a sharp point in a NURBS curve ¶
Sometimes you want to create a sharp corner in a NURBS curve. You can do this in the following ways:
-
Change the weight of a selected CV via the Curve > Parameters dialog in the Model Editor to something high like 10,000. This gives the CV so much “pull” that it draws the curve almost right through it.
-
If you drag the two adjacent CVs of a cubic curve onto a middle CV, it will look like a sharp corner point. This is called raising the multiplicity of the CV. Maximum CV multiplicity occurs when adjacent “degree” CVs overlap.
-
Make “degree” knots identical. This is called raising the multiplicity of the knot. You can do this in the
Refine SOP by choosing the Subdivide option, or in the Model Editor by selecting the Refine state and dividing with
.
Quadratic primitive shapes ¶
Houdini supports primitive spheres/ellipsoids, circles/ellipses, and tubes/cones. These shapes are defined by very simple mathematical parameters (for example, height and width) and a single center-point vertex. They can be moved, rotated, and scaled.
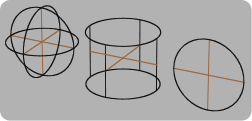
Quadratic primitives are extremely lightweight, and work well in applications such as:
-
Showing hundreds of thousands or millions of copies of simple shapes, as in
instancing.
-
Stand-in geometry.
-
Envelope geometry (for example, for bouncing particles off of).
Many modeling tools work on quadratic primitives, but the primitives do not have any topology, so operators that act on surface points will not work with quadratic primitives.
| See also |