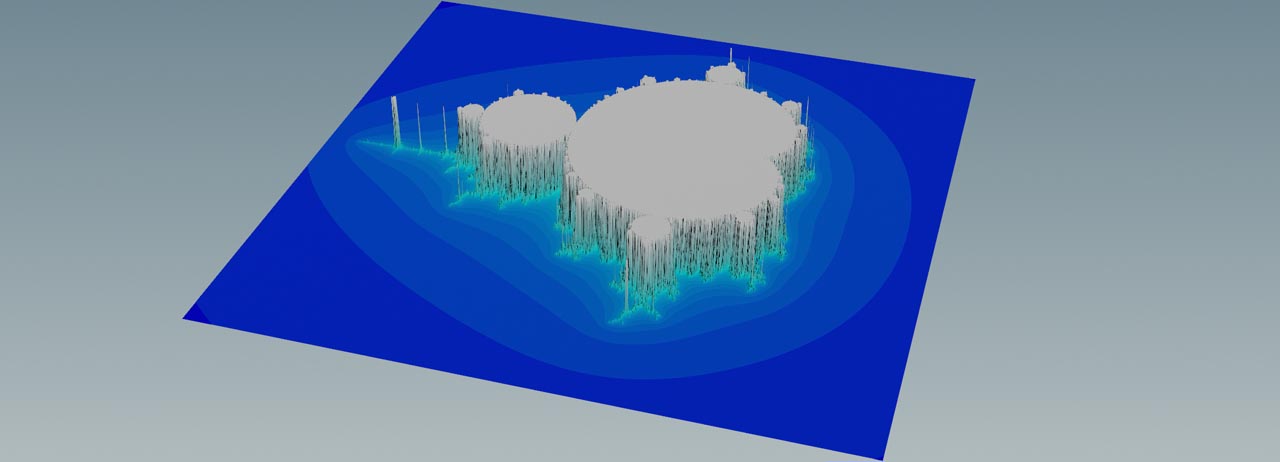
This example is just to illustrate that you can do pretty fancy things with Houdini’s heightfields. You might have heard about the so-called Mandelbrot set. The name giver is Benoit B. Mandelbrot , a Polish-French-American mathematician. The Mandelbrot set is a self-similar fractal that’s based on complex numbers. The iconic element of the Mandelbrot set is a black area that reminds of an apple. The structures around the “apple” are color-coded to make them differentiable. Self-similarity means that you can “dive” into the fractal to reveal more detail, but you’ll always see very similar patterns. The level of detail depends on the number of iterations.

With heightfields and VEX it’s possible to translate the fractal patterns into height information and create a Mandelbrot-style landscape. Here’s the script without further explanation. There’s plenty of information about fractals in general and the Mandelbrot set on the internet.

// Parameter definition int maxiter = chi("iterations"); float scale = 1 / chf("scale"); float offset_x = chf("offset_x"); float offset_z = chf("offset_z"); float escape_threshold = chf("escape_threshold"); float amplifier = chf("amplifier"); float core_height = chf("core_height"); // Main rountine 'mandelset' function float mandelset(float x0, y0; int imax; float escape) { float x = 0; float y = 0; float xnew, ynew; int i; for (i = 0; i < imax; i++) { xnew = x * x - y * y + x0; ynew = 2 * x * y + y0; if (xnew * xnew + ynew * ynew > escape) { return float(i) / float(imax); // Normalized iteration depth } x = xnew; y = ynew; } return -1.0; // Points within in the Mandelbrot set } // Mandelbrot calculation float value = mandelset(@P.x * scale - offset_x, @P.z * scale - offset_z, maxiter, escape_threshold); if (value >= 0) { @height = value * amplifier; @height += sin(value * 10) * 0.1; // Bands } else { @height = core_height; }
Parameters ¶
The script is rather short, but provides a several parameters that let you customize the fractal. The last numbers in the table below are example values that produce a “standard” Mandelbrot set. On the Heightfield Wrangle SOP
| Parameter | Description | Value |
|---|---|---|
| Iterations | The fractal’s “resolution”. Higher values take longer to calculate, but create more details. Note that the amount of visible structures also depends on the heightfield’s grid size. |
200
|
| Scale |
The size of the Mandelbrot set. You typically need values of 100 and more to see the fractal’s structures.
|
300
|
| Offset X/Z |
The Mandelbrot set’s normalized position. Normalized means that the offset values range between 0 and 1. A value of 0.5 represents the midpoint.
|
0.5 / 0
|
| Escape Threshold | Determines, when a point is no longer considered a part of the Mandelbrot set. This parameter creates the banding effect around the fractal. Higher values create more details, but take longer to calculate. |
800
|
| Amplifier | A scale factor for the structures outside a apple-shaped area. High values create the typical spikes. |
75
|
| Core Height | The height of the apple-shaped area in meters. |
100
|
With the values above you get the image shown below. Height information is color-coded here with a HeightField Visualize SOP.