| On this page |
|
L-Systemsについて ¶
L-Systems( Lindenmayer-systems のことで、Aristid Lindenmayer,1925-1989の名前が由来です)では、 反復処理によって複雑な形状を定義することができます。 このシステムは、数学的な言語を使用していて、そこで使用する初期の文字列が反復処理のルールに相当し、 その結果からジオメトリを生成します。 各ルールの評価の結果が次の反復の形状の基本となって、まるで成長しているかのような錯覚になります。
L-system SOPは、木、稲妻、雪の結晶、花、他の枝分かれする現象などの複雑な有機的な構造をシミュレーションすることができます。
ビューアにL-Systemを配置 ¶
フラクタルの特性 ¶
植物の構造を体系化して、美しく見せるための組み合わせの要因がいくつかあります。それらの要因が以下の通りです:
-
対称
-
自己相似性
-
成長アルゴリズム
私達はL-System対して主に後者の2つの要因に関心があります。 自己相似性とは、L-Systemで文字列を使うことでフラクタル構造を表現することができます。 マンデルブローは以下のようにして自己相似性を記述します:
“各形状が幾何学的に全体の形状と似ている時、それらを自己相似性と呼びます。”
L-Systemsでは、時間に渡って自己相似性の成長を記述するための文法があります。 L-Systemsのルールは、基本となる成長構造を化学的な成長を決めるDNAのように決めます。 この成長は、自己相似性の構造に基づいて簡単な記述をするだけで、複雑なサーフェスを表現することができます。
書き換え ¶
L-Systemsの主な概念は、 書き換え です。これは、初期状態( Initiator )を、書き換えるジオメトリ( Generator )で置換することで再帰的に動作します。 そして、置換する間隔と同じポイントを持つように減らして移動します。
1968に、Astrid Lindenmayerは、その文字列書き換えの仕組みを“L-Systems”という用語として紹介しました。 L-Systemsの文法は独特で、生成する方法が並列的で、指定した“単語”内のすべての文字を同時に置換します。
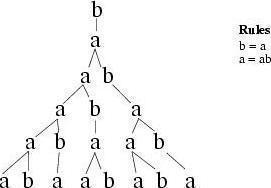
書き換えの構文の一番単純な例は、2つの“単語”の組み合わせで構築します。つまり、aとbを何度も文字列内に記述します。
各文字が、書き換えルールに関連しています。a = abは、文字aが文字列abに置換され、b = aは、文字bが文字aに置換されることを意味します。
文字bで処理を始めて( Premise )、時間に渡って、その文字に従うとすれば、書き換えルールに基づいて、あるパターンの生成を確認することができます:
生成ルールの構文 ¶
L-Systemsのルールの一般書式:
[left_context<] symbol [>right_context] [:condition]=replacement [:probability]
意味…
left_context
このルールのマッチングに対して‹symbol›の前に付く任意の文字列。
symbol
置換するシンボル。例えば、Aであれば、初期文字列内のAが(このルールにマッチすれば)‹replacement›に置き換えられます。
right_context
このルールのマッチングに対して‹symbol›の後に付く任意の文字列。
condition
このルールのマッチングでtrueになる任意のエクスプレッション。
replacement
(このルールにマッチすれば)‹symbol›を置換する文字列。
probability
このルールが実行される任意の可能性(0から1の間)。
例えば、0.8であれば、時間の80%で、このルールが実行されます。
Tip
生成ルールには、=ではなく->を使うことができます。これは同等を意味します。
タートルコマンド(文字指定による描画) ¶
この文字列操作システムとグラフィックルーチンによって、位置(XYZ)と向き(角度)を文字列として指定することで、画面上に線を描画することができます。
単純なタートルコマンドの例:
F
一歩移動して、前の位置から今の位置までを直線で繋ぎます。
f
描画しないで一歩移動します。
+
右に90度回転します。
-
左に90度回展します。
(実際のL-Systemノードでは、+と-コマンドの角度を調整することができます)
この単純なルールによって、簡単にL字のような形状を文字列を指定して描画することができます。 例えば、タートルコマンドの初期状態が上方向を向いていると仮定した場合、以下の文字列によってL字を描画することができます:
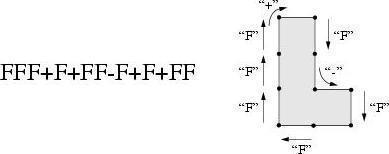
タートルコマンド文字列の書き換え ¶
タートルコマンドの文字列を書き換えルールで繰り返して実行することで、驚くほどに複雑な形状を生成することができます。 書き換えルール内の自己参照の威力は、非常に複雑な図形を作成することができます。
非常に単純な自己参照の使い方の例として、L-Systemに初期文字列をAに、ルールをA=F+Aと仮定します。このルールの意味は、
“'A'を見つければ、その文字を'F+A'に置換する”ということです。置換する文字列には、置換元の文字を含んでいるので、これは、 直列効果 で文字列が展開されていきます:
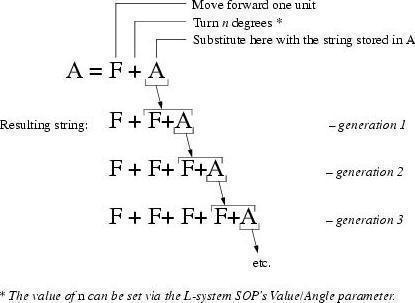
これは、“一歩進んで、回転する”を繰り返した成長リストを生成します。 90未満の回転角度と十分な数のジェネレーションを指定すれば、このL-Systemは、円弧や円を近似します。 この挙動を利用すれば、1枚の紙を丸めたり、サソリの尻尾を丸めることができます。 また、回転角度をランダムにすれば、曲がりくねった線を作成することができるので、稲妻を作成することができます。
(タートルコマンド文字列F+Aを数学の F 足す A と混同しないでください。L-Systemsのコンテキストでは、+は“加算”ではなくて“回転”を意味します。)
他の例: 以下の図形は、 二次コッホ曲線 と呼ばれているものです:
| 初期文字列(Premise) |
|
| 書き換えルール |
|
| 角度 |
|
このタートルコマンドは、3回のジェネレーションで以下の図形を生成します:



Note
指数関数的に生成される数が増えていくので、Houdiniでこのコッホ曲線を試す際は、 Generations パラメータを3よりも大きくしないでください。
Tip
L-Systemノード上をクリックすれば、ノードの現在の文字列を確認することができます。これは、ルールのデバッグで非常に役に立ちます。
枝分かれ ¶
L-Systemsはたくさんの単一接続の直線を生成することができます。木のように枝分かれさせるには、 枝 を作成する必要があります。
L-Systemsは、大括弧([と])で枝を作成することができます。大括弧内に記述したタートルコマンドは、メインの文字列とは別に新しいタートルとして実行されます。
例えば、タートルコマンドF [+F] F [+F] [-F]は以下のように解釈されます:
-
一歩移動します。
-
新しいタートルで枝分かれして、右に回転して一歩移動します。
-
一歩移動します。
-
新しいタートルで枝分かれして、右に回転して一歩移動します。
-
新しいタートルで枝分かれして、左に回転して一歩移動します。
このタートルコマンドは、以下の図形を作成します:
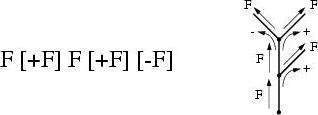
他の例: タートルコマンドF [+F] [-F] F [+F] -FFは、以下の図形を作成します:

3D ¶
L-Systemsは、平坦なジオメトリをたくさん作成します。
3Dでジオメトリを作成するには、^ (ピッチアップ), & (ピッチダウン), \ (時計回りにロール), / (反時計回りにロール)コマンドを使います。
例えば、初期状態FFFAと以下のルールでは:
A= " [&FFFA] //// [&FFFA] //// [&FFFA]
これは以下の処理をします:
|
現在の岐の長さをスケールします。 |
|
ピッチダウン( |
|
反時計回りに4回ロールします。 |
これは、以下の3D図形を作成します:
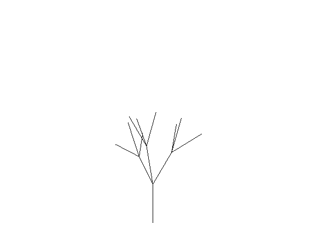
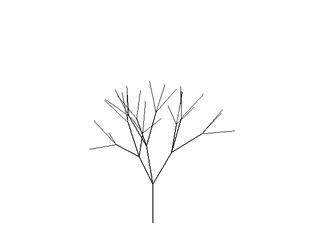



そのルールは、ジェネレーション毎に3つの枝を作成します。ピッチダウンコマンド(&)は、枝を垂直に分割します。ロールコマンド(/)は、異なる方向に枝を向けます。
(各枝の最後のAは、そのルールの新しいコピーが最後の枝から成長します。)
"コマンドは、生成毎にFコマンドを半分の長さにします。これは、枝を短くするのに便利です。
複数のL-Systemルールを使用する ¶
前の章では、ルールにA= " [&FFFA] //// [&FFFA] //// [&FFFA]を使いました。
このルールには、明らかに冗長性があります。L-Systemsは、シンボルを文字列で置換するので、単に繰り返し文字列をシンボルで置換して、そのシンボル用の新しいルールを作成することができます:
Rule 1 |
|
Rule 2 |
|
枝が一箇所で定義されているので、枝の命令を変更したいのであれば、1つの文字列だけを編集する必要があります。
2つのルールのシステムは、同じ結果のジェネレーション回数と比べて 2倍のジェネレーション回数 が必要です。 これは、各ジェネレーションが、1つのルール代入を実行しているのが原因です。
つまり、単一ルールのA= " [&FFFA] //// [&FFFA] //// [&FFFA]がジェネレーション毎にAを展開して成長するのに対して、A= " [B] //// [B] //// [B]とB= &FFFAの2倍のルールは、Aを" [B] //// [B] //// [B]に置換して、Bを&FFFAに置換して動作しています。
タートルコマンドのリファレンス ¶
通常では、タートルコマンドは、現在の長さ/角度/厚みなどを使って、エフェクトを決めます。 括弧内に引数を明示すれば、タートルコマンドで使われている標準値を上書きすることができます。
以下のリストには、括弧で閉じた引数を載せています。引数なしで単一文字コマンドだけを使えば、Houdiniは標準値だけを使うことを忘れないで下さい。
括弧内の引数のエクスプレッションで使用可能な関数と変数に関しては、以下のローカル関数とローカル変数を参照してください。
F(l,w,s,d)
距離‹l›、幅‹w›、分割数‹d›、断面数‹s›で一歩移動(ジオメトリを作成)します。
H(l,w,s,d)
距離‹l›、幅‹w›、分割数‹d›、断面数‹s›で半歩移動(ジオメトリを作成)します。
G(l,w,s,d)
距離‹l›、幅‹w›、分割数‹d›、断面数‹s›で一歩移動しますが、頂点を記録しません。
f(l,w,s,d)
距離‹l›、幅‹w›、分割数‹d›、断面数‹s›で一歩移動(ジオメトリを作成しません)します。
h(l,w,s,d)
距離‹l›、幅‹w›、分割数‹d›、断面数‹s›で半歩移動(ジオメトリを作成しません)します。
J(s,x,a,b,c), K(s,x,a,b,c), M(s,x,a,b,c)
ジオメトリのスケール、向き変更の後のタートルの位置でリーフ入力J、K、Mからジオメトリをコピーします。 ジオメトリをsパラメータ(デフォルトはStep Size)でスケールして、‹c›の‹a›値でスタンプします(デフォルトはスタンプなし)。 スタンプは、指定したパラメータが存在して、それに関連するLeafパラメータが設定されていると発生します。 ‹x›パラメータを使わないなら、0に設定します。Leaf入力内のPointベクトルアトリビュートは、タートルの移動で影響を受けることに注意してください。
T(g)
屈性ベクトル(重力)を適用します。この角度は、マイナスY軸に向かいます。変化量は、‹g›で制御します。デフォルトの変化量は、Gravityパラメータを使います。
+(a)
右に‹a›度回転します。デフォルトはAngle。
-(a)
左に‹a›度回転します。デフォルトはAngle。
&(a)
‹a›度ピッチダウンします。デフォルトはAngle。
^(a)
‹a›度ピッチアップします。デフォルトはAngle。
\\(a)
時計回りに‹a›度ロールします。デフォルトはAngle。
/(a)
半時計回りに‹a›度ロールします。デフォルトはAngle。
|
180度回転します。
*
180度ロールします。
~(a)
‹a›度までランダムにピッチ/ロール/回転します。デフォルトは180。
"(s)
現行の長さをsで乗算します。デフォルトはStep Size Scale。
!(s)
現行の厚みをsで乗算します。デフォルトはThickness Scale。
;(s)
現行の角度をsで乗算します。デフォルトはAngle Scale。
_(s)
現行の長さをsで割算します。デフォルトはStep Size Scale。
?(s)
現行の幅をsで割算します。デフォルトはThickness Scale。
@(s)
現行の角度をsで割算します。デフォルトはAngle Scale。
'(u)
‹u›でカラーインデックスUを上げます。デフォルトは、 UV Increment の1番目のパラメータ。
#(v)
‹v›でカラーインデックスVを上げます。デフォルトは、 UV Increment の2番目のパラメータ。
%
残りの枝を切り落とします。
$(x,y,z)
Upベクトルが(0,1,0)になるようにタートルを回転します。タートルをポイント(x,y,z)の方向に向けます。デフォルトの挙動は、向きのみで方向を変更しません。
[
タートルの状態をプッシュします(枝を開始します)。
]
タートルの状態をポップします(枝を終了します)。
{
ポリゴンを開始します。
.
ポリゴン頂点を作成します。
}
ポリゴンを終了します。
g(i)
結果のジオメトリを追加するための新しいプリミティブグループを作成します。グループ名は、Group Prefixの後に番号‹i›が付きます。 パラメータを指定しなかった場合のデフォルトは、現行グループ番号でグループを作成して、現行グループ番号を上げます。
a(attrib, v1, v2, v3)
これは、nameアトリビュートのPointアトリビュートを作成し、この枝上の残りのポイントに対して他のコマンドがリセットするまでv1, v2, v3に設定します。
‹v2›と‹v3›は任意です。それらの引数が存在しなかった場合は、少ないfloatでアトリビュートが作成されます。
作成されるアトリビュートは、常にfloatタイプで、デフォルトが0です。例えば、Premiseの開始に追加したルールa("Cd", 1, 0, 1)は、L-Systemを魅力的な紫色にします。
ローカル関数とローカル変数 ¶
これらの関数と変数は、F()などのタートルコマンドの引数で利用可能です。
これらは、パラメータエクスプレッションの関数とは異なり、ノードローカル変数です。
acos(v)
アークコサイン。コサインの逆数。単位が度で結果を返します。
asin(v)
アークサイン。サインの逆数。単位が度で結果を返します。
cos(angle)
コサイン。単位が度で角度を受け取ります。
sin(angle)
サイン。単位が度で角度を受け取ります。
chan(idx)
このノードの現行時間におけるアニメーションSpareパラメータの値を返します。
このノードにSpareパラメータを追加し、そのパラメータにキーフレームを打ってから、そのアニメーション値を使って時間軸でL-Systemを変更することができます。
LSystem channel prefix パラメータを使って、このSpareパラメータの名前を指定してください。
例えば、spareという名前のSpareパラメータタプルを追加して、 Lsystem channel prefix にspareを設定したとします。
このspareの1番目のコンポーネントの値(現行フレーム時間)を参照したいのであれば、chan(0)を使用します(これは、spare0という名前のチャンネルを評価します)。
2番目のコンポーネントにアクセスするには、chan(1)を使用します。3番目のコンポーネントならchan(2)です。
min(a, b)
aまたはbの小さい方を返します。
max(a, b)
aまたはbの高い方を返します。
in(x, y, z)
これは、(x, y, z)のポイントがMeta Test Input内にあるかどうかを判断します。
pic(x, y, plane)
これは、(x, y)座標におけるL-System Pictureを評価します。この値の範囲は0..1です。
plane
取得したい画像チャンネル。0 = 輝度, 1 = 赤, 2 = 緑, 3 = 青。
0..1の範囲の値を返します。
rand(seed)
randエクスプレッション関数と同じです。
rand(i)を使用することで簡単に乱数を取得することができます。
a
L-Systemのangleパラメータ。
b
L-Systemのbパラメータ。
c
L-Systemのcパラメータ。
d
L-Systemのdパラメータ。
g
初期が0です。その後に、現行ルールの寿命が設定されます。
i
ルールを適用する現行L-System文字列のオフセット。
t
初期が0です。その後に、繰り返し回数が設定されます。
x, y, z
空間内の現行タートル位置。
A
木の根から現行ポイントまでの円弧長。
L
そのポイントでの現行長さインクリメント。
T
L-Systemのgravityパラメータ。
U
カラーマップのU値。
V
カラーマップのV値。
W
現行ポイントでの幅。
L-Systemにモデリングしたジオメトリを使用する ¶
Houdiniでは、あるコマンドを使うことで、タートルの位置にジオメトリのコピーを作成することができます。 これによって、例えばL-Systemの低木に葉っぱと花を作成することができます。
-
スタンプしたいジオメトリの出力をL-Systemノードの入力の1つに接続します。
-
タートルコマンド内に入力に相当するコマンド(
J、K、M)を使って、ジオメトリを挿入します。
入力 |
タートルコマンド |
|---|---|
1 |
|
2 |
|
3 |
|
L-Systemの入力1に葉っぱのジオメトリを、入力2に花のジオメトリを接続する場合は、以下の設定にすることで、葉っぱと花で埋められた茂みを作成することができます:
Premise |
|
Rule 1 |
|
Rule 2 |
|
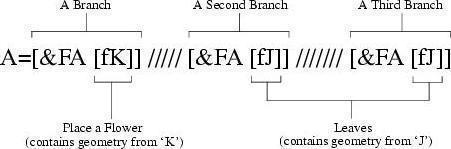
Rule 1では、KとJの前にf(描画しないで移動)を付けて、少しだけジオメトリをオフセットします。
そうしないと、葉っぱが線の端ではなく中心に取り付けられてしまいます。
シンボル変数 ¶
各シンボルには、ユーザ定義変数を5つまで関連付けることができます。 それらの変数は、エクスプレッションで参照または割り当てをすることができます。 マッチしたシンボル変数がインスタンス化されると同時に、replacement内の変数が割り当てられます。
例えば、A(i, j)=A(i+1, j-1)のルールは、各Aを、1番目のパラメータ(i)を1上げて、2番目のパラメータ(j)を1下げる新しいAに置換します。
ジオメトリのシンボル(例えば、F, +、!)に割り当てたパラメータは、幾何学的に解釈されます。例えば、F(i, j) = F(0.5*i, 2*j)のルールは、再度、各Fを修正したパラメータを含む新しいFに置換します。
さらに、新しいFは、半分の長さと2倍の幅で描画します。
Tip
前の変数をルールの条件や可能性の割合で参照することもできます。例えば、A(i):i<5 = A(i+1) A(i+1)のルールは、最大5倍で各Aを倍にします(PremiseをA(0)と仮定)。
時間の経過と共に長さを制御する ¶
繰り返す度に‹x›パーセント小さく移動するL-Systemを作成するには、Puremiseに値を設定して、残したいパーセンテージ分の値を乗算するルールを設定する必要があります。
Premise |
|
Rule |
|
‹A›の前に‹i›をスケールするこの方法は、再評価されます。重要な部分はPremiseです。それをスケール可能な値で始める必要があります。
入力ジオメトリ上のスタンプ変数 ¶
J/K/Mコマンドの3番目の引数を、接続するジオメトリへ渡します。
Tip
この裏技を使えば、L-Systemの3つだけのジオメトリ入力の制限を回避することができます。
欲しい異なるモデルすべてを作成し(つまり、20種類の葉っぱ)、それらをSwitchノードに接続します。Switchノードの Select Input パラメータを
stamp("/path/to/lsystem", "lsys",0)に設定します。
SwitchノードをL-SystemノードのJ入力に接続します。J(L,0,‹leaf_number›)を使えば20種類の葉っぱのどれかを挿入することができます。
-
Circleノードを作成して、分割数を
stamp("/path/to/lsystem", "lsys", 3)に設定します。デフォルトの分割数は3(エクスプレッション内の2番目の引数)なので、これは三角形を作成します。
-
Circleノードの出力をL-SystemノードのJ入力に接続します。
-
L-Systemルールでは、
J(L,0,‹number›)を使って、‹number›をJジオメトリに渡すことができます。例えば、J(L,0,4)は正方形を生成し、J(L,0,5)は五角形を生成します。
L-Systems内にグループを作成する ¶
gコマンドは、現在構築しているジオメトリすべてをグループに格納します。
グループ名は、 Funcs タブのプリフィックスと番号で構成されます。
デフォルトのプリフィックスはlsysで、“lsys1”のようなグループ名を生成します。gコマンドには、引数として番号を指定することができます。
例えば、g[F]は、Fのジオメトリをグループに格納します。デフォルトのインデックスは、適切にインクリメントされます。
現行グループは、枝と関連付いているので、gF [ gFF ] Fのように実行すれば、最初と最後のFをgroup 0に、中間の(枝の)FFをgroup 1に格納することができます。
その親のグループから枝を排除するには、g(-1)を使います。
エッジの書き換え ¶
The Algorithmic Beauty of Plants のたくさんのサンプルには、 エッジの書き換え というテクニックを使っています。これは、左右のサブスクリプトが必要です。基本的なサンプル:
Generations |
|
Angle |
|
Premise |
|
Rule 1 |
|
Rule 2 |
|
しかし、Houdiniでは、F(l)とF(r)の構文をサポートしていません。その代わりに、ルールを修正することでシンボル変数を使うことができます。
Fタートルシンボルでは、最初の4つのパラメータは、‹length›、‹width›、‹tubesides›、‹tubesegs›です。最後のパラメータは、ユーザ定義可能です。 0が左、1が右になるように、この最後のパラメータを定義することができます:
Generations |
|
Angle |
|
Premise |
|
Rule 1 |
|
Rule 2 |
|
2つのジェネレーションの後は、これはFl+Fr+-Fl-Frを生成します。この最後の文字列とF+F+-F-Fには違いはありません。
他の方法は、2つの新しい変数を使って、最後のステップで条件分を使って、それらをFに変換することです:
b |
|
Premise |
|
Rule 1 |
|
Rule 2 |
|
Rule 3 |
|
Rule 4 |
|
以下の出力を生成します:
Generation |
String |
|---|---|
0 |
|
1 |
|
2 |
|
3 |
|
形状内にL-Systemの成長を制限する ¶
L-SystemノードのMeta Test Inputでは、システムが造園のような定義した形状に到達した時に、そのシステムを停止させるルールを生成することができます。
-
L-Systemが成長できる範囲のボリュームを定義するために、メタボールまたは結合したメタボールを作成します。
-
メタボールノードの出力をL-SystemノードのMeta Test Inputに接続します。
-
条件ステートメント(
:)を“in”テストと一緒に使います。例:
サンプル ¶
Premise |
|
Rule 1 |
|
Rule 2 |
|
-
このL-Systemは、次の成長の繰り返しがMeta Test境界内にあるかどうかチェックします。境界内になければ、現行の枝を切り捨てます。
-
Rule 1は、枝がMeta Test境界内にある時に80%の回数を実行します。
-
Rule 2は、枝がMeta Test境界内に ない 時に実行します(
!は、in(x,y,z)条件を否定します)。%コマンドは、枝を終了します。
Note
L-System開始点が、メタボールエンベロープ内にない場合は、休止状態になります。 L-Systemとメタボールをセットアップしてしまえば、L-Systemが不意にメタボール外に移動しないように、それらが一緒にトランスフォームするようにしてください。
L-Systemsでジオメトリインスタンスを配置 ¶
L-Systemsは、モデリングしたジオメトリを配置するのに強力なツールです。 L-SystemをCopy SOPのテンプレート入力として使用することで、L-Systemのすべてのポイントにモデルをコピーすることができます。
例えば、L-systemの基本(premise=A, rule=A=F+A)の“円弧近似”のL-Systemを使えば、円弧の曲率と間隔を制御してモデルを配置することができます。
参考文献 ¶
L-Systemsに非常に興味があれば、以下の書籍を参考にしてください:
Przemyslaw PrusinkiewiczとAristid Lindenmayerが著書の The Algorithmic Beauty of Plants (1996, Springer-Verlag, New York. Phone 212.460.1500. ISBN: 0-387-94676-4)
この本はL-Systemsの決定本です。たくさんのL-Systemsのサンプルと、リアルな植物の成長をモデリングするためのアイデアと理論が掲載されています。
計算の高速化 ¶
全体の木のように単一の大きなL-Systemでモデリングすると、衝突計算では単体として扱われてしまいます。Wire Solverは、個々に計算できるようにWireオブジェクトを部分毎に検索して、作業単位を複数に分割します。1つの大きく接続されたL-Systemは、より小さな作業単位に分割することができません。
Wire Glue Constraint DOPを使って、木の根付近の枝の継ぎ目のL-Systemのポイントを拘束してみてください(ポイントをそのワールド空間位置に拘束)。これによって、Wire Solverが離れた枝を個々に計算可能な別の部分として見るようになります。拘束したポイントは動かないので、枝の1つの動きが、他のブランチに影響を与えません。可能であれば、Wireオブジェクトのポイント数を減らすことで、計算が高速化されます。
パラメータ ¶
Geometry ¶
Type
タートル移動した時に作成するジオメトリのタイプ。
Tip
Polywire SOPを使ってスケルトンL-Systemからチューブパスを作成することができます。
Skeleton
ポリラインの描画。
Tube
チューブの描画。
Generations
ルールの代入の繰り返し回数。小数点を指定して 以下の Continuous Angles 、 Continuous Length をオンにした場合、Houdiniは、ジェネレーション間で滑らかに成長するように、最後の代入で生成されるジオメトリをスケールします。
Start Position
これは、タートルの開始点の位置です。
Random Scale
ゼロ以外の値であれば、Fやそれと同様のタートル関数で指定した長さすべてをランダムにスケールします。
Random Seed
乱数生成で使用するシード値。ランダムルール(つまり、Randome Scale、~、確率的ルール)を使用するL-Systemに対して、この値を変化させることで、ルールが他のL-Systemのインスタンスを生成することができます。
Continuous Angles
設定すると、最後のジェネレーションのタートル操作で回転する角度が、Random Scaleの値でスケールして生成されます。
Continuous Length
設定すると、最後のジェネレーションのタートル操作で移動する長さが、Random Scaleの値でスケールして生成されます。
Continuous Width
設定すると、最後のジェネレーションのタートル操作で生成する幅が、Random Scaleの値でスケールして生成されます。
Apply Color
設定すると、L-Systemは、各ポイント上のカラーアトリビュートを出力します。 カラー値は、現行UV位置でのImage Fileでの色になります。現行UV値は、'と#のタートル操作で修正することができます。
Image File
これは、 Apply Color で使用する画像ファイルです。 pic()エクスプレッションで使用する画像ファイルは、 Funcs タブにあります。
UV Increment
これらの値は、'と#のタートル操作のデフォルトのUとVのインクリメントを決めます。
Point Attributes
タイプがSkeletonなら、このパラメータが利用可能です。このパラメータをオンにすれば、各ポイントがどのように生成されたのか追跡するために、たくさんのPointアトリビュートを作成します:
width
生成されたチューブの幅。
segs
チューブで作成されたセグメント数。
div
チューブの分割数。
lage
木の根から垂直のインクリメント。これは、 Tube タブの Vertical Increment パラメータから影響を受けます。
arcと同様ですが、エッジの長さに依存しません。
arc
タートルパスの根からこのポイントまでの円弧長。
up
このポイントでのタートルのUpベクトル。
gen
このポイントを作成したジェネレーション。
Tube ¶
Rows
チューブの横方向の分割数。値を3にすれば、チューブは三角形にスイープします。
Cols
チューブの縦方向の分割数。値を4にすれば、1つのFで4つの断面を作成します。
Tension
チューブの目的の位置までのスイープの真っ直ぐさの度合い。
Branch Blend
新しい枝が古い枝の方向を引き継ぐ度合い。
Thickness
デフォルトのチューブの幅。
Thickness Scale
!オペレーションがThicknessに与える影響の度合い。
Apply Tube Texture Coordinates
チェックすると、チューブは、UVテクスチャ座標を生成します。
Vertical Increment
各チューブがVテクスチャ座標をインクリメントする量。
Values ¶
Step Size
Fコマンドなどの移動のデフォルトサイズ。
Step Size Scale
"コマンドで使用する数。
Angle
/コマンドなどのデフォルトの角度。これは、エクスプレッション変数aにもなります。
Angle Scale
;コマンドで使用する数。
Variable b
エクスプレッション変数bの値。
Variable c
エクスプレッション変数cの値。
Variable d
エクスプレッション変数dの値。
Gravity
Tコマンドの屈性量。これは、エクスプレッション変数Tの値にもなります。
Number Of Variables
このMultiparmには、任意の数の新しいエクスプレッション変数の割り当てが可能です。
Variable Name
エクスプレッション変数名。これは、単一文字です。 既に予約されている変数を確認するには、以下の ローカル変数 のセクションをチェックしてください。
Variable Value
エクスプレッション変数の値。
Funcs ¶
Pic Image File
pic()エクスプレッション関数で使用する画像ファイル。
Group Prefix
gコマンドで使用するプリフィックス。
Channel Prefix
chan()エクスプレッション関数で使用するプリフィックス。
Leaf Param A
これは、Leafをスタンプするスタンプパラメータの名前です。 スタンプの値は、J、K、Mの操作で決まります。 stamp()関数を使って上流の値を読み込むことができます。
Leaf Param B
これは、Leafをスタンプするスタンプパラメータの名前です。 スタンプの値は、J、K、Mの操作で決まります。 stamp()関数を使って上流の値を読み込むことができます。
Leaf Param C
これは、Leafをスタンプするスタンプパラメータの名前です。 スタンプの値は、J、K、Mの操作で決まります。 stamp()関数を使って上流の値を読み込むことができます。
Rules ¶
Read Rules From File
これを設定すれば、Ruleフィールドが無視されます。その代わりに、 Rule File のファイルがルールとして使われます。
Write Rule Parameters to File
これは、現行ルールすべてをRule Fileに書き出します。
Rule File
ルールのソースとして使用するファイル名。このファイルには、1ルール1行を記述します。 空行と'#'で始まる行は無視されるので、'#'を使えばコメントを追加することができます。
Context Ignore
これはシンボルのリストです。これらのシンボルは、コンテキストを決めようとした時に無視されます。
Context Includes Siblings
デフォルトでは、各枝のコンテキストのみが、その枝にそのシンボルを含みます。
サブ枝または親の枝はスキップされます。
A>B=F, A[B]のルールを指定すると、Bがサブ枝内の時には、そのルールは計算されません。
[Q]が無視されるのでA[Q]Bは、計算されます。Context Ignoreを[]に変更すると、この効果が削除されて、A[Q]Bは計算されませんが、A[B]は計算されます。
例えば、[A]Q[B]は、このフラグを設定すれば計算されますが、設定しなかった場合は計算されません。
Premise
L-Systemの初期状態。これは、ジェネレーション0でのL-Systemの状態です。
Rule #
L-Systemに適用するルール。トグルをオフにしてルールを無効化すれば、ジェネレーションプロシージャから、そのルールを削除されます。
入力 ¶
Leaf J
このジオメトリは、Jのルールで使われます。
Leaf K
このジオメトリは、Kのルールで使われます。
Leaf M
このジオメトリは、Mのルールで使われます。
Meta Test Input
このジオメトリは、境界領域をチェックするin()関数で使われます(造園用).
Examples ¶
LSystemMaster Example for L-System geometry node
L-System SOPは、反復処理によって複雑な形状を定義することが可能です。このノードは初期文字列を繰り返して評価する数学的な言語を使用し、その評価結果からジオメトリを生成します。各評価の結果が次のジオメトリの反復の基本になり、ジオメトリが成長していきます。
このサンプルのネットワークは、あなたが初めてL-Systemの独自ルールを記述するのに十分です。
しかし、L-Systemの作成に本気で興味のある人は次の本を読むべきです:
The Algorithmic Beauty of Plants, Przemyslaw Prusinkiewicz and Aristid Lindenmayer
L-Systemのコマンドの完全なリストは、Houdiniのヘルプを参照してください。

LsystemBuilding Example for L-System geometry node
このサンプルは、L-System SOPを使って窓のあるビルを生成する方法を説明しています。

| See also |
